A number  is called practical if all the numbers
is called practical if all the numbers  can be written as the sum of distinct proper divisors of
can be written as the sum of distinct proper divisors of  .
.
![\[
p_j \le 1 + \sigma(p_1^{e_1}\cdots p_{j-1}^{e_{j-1}})\,,
\]](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93d3cubnVtYmVyc2FwbGVudHkuY29tL3NldC9wcmFjdGljYWxfbnVtYmVyL3BpYy43LnBuZw%3D%3D) where
where 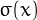 denotes the sum of divisors of
denotes the sum of divisors of  .
.

For example, 18 is practical because every smaller number can be written as a sum of its proper divisors, 1, 2, 3, 6, 9, like 13=1+3+9.
Steward and Sierpiński have characterized completely the set of
practical numbers as follows. A number 1$">, whose prime factorization
is
is a practical number if and only if
it is even (i.e.,
) and, for every
, it holds
The first practical numbers are 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150, 156, 160 more terms
Below, the spiral pattern of practical numbers up to . See the page on prime numbers for an explanation and links to similar pictures.
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

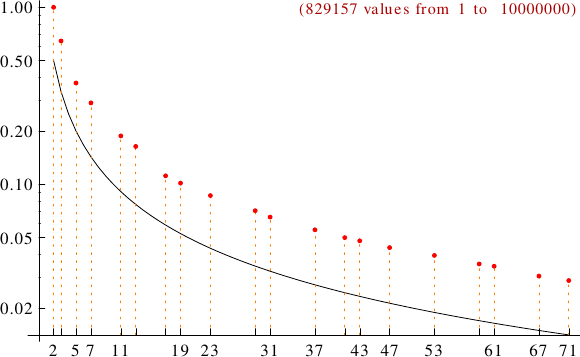
A graph displaying how many practical numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Practical numbers can also be... (you may click on names or numbers and on + to get more values)
ABA
18
24
32
+
9999392
aban
12
16
18
+
10000000
abundant
12
18
20
+
10000000
Achilles
72
108
200
+
9999392
admirable
12
20
24
+
9989312
alternating
12
16
18
+
8989890
amenable
12
16
20
+
10000000
amicable
220
1184
17296
+
9363584
apocalyptic
192
220
224
+
30000
arithmetic
20
30
42
+
9999990
astonishing
204
216
3078
+
2282148
Bell
4140
betrothed
48
140
1050
+
8829792
binomial
20
28
36
+
9965880
c.heptagonal
736
3256
7568
+
9304856
c.nonagonal
28
496
820
+
9823528
c.pentagonal
16
276
456
+
9815856
c.triangular
64
460
760
+
9696460
cake
42
64
176
+
9963072
Catalan
42
132
208012
+
2674440
compositorial
24
192
1728
+
2903040
congruent
20
24
28
+
9999990
constructible
12
16
20
+
8947712
cube
64
216
512
+
9528128
Cunningham
24
28
48
+
9991920
Curzon
18
30
54
+
9999990
d-powerful
24
132
224
+
9997668
decagonal
126
540
1242
+
9880020
deficient
16
32
64
+
8388608
dig.balanced
12
42
56
+
9999990
double fact.
48
384
3840
+
645120
droll
72
240
672
+
9461760
Duffinian
16
32
36
+
9999392
eban
30
32
36
+
6066060
economical
16
32
64
+
10000000
enlightened
256
2048
2176
+
2560000
equidigital
16
32
64
+
9999936
eRAP
20
24
1104
+
9952712
esthetic
12
32
54
+
8765456
Eulerian
66
120
14608
+
2203488
evil
12
18
20
+
10000000
factorial
24
120
720
+
3628800
fibodiv
28
3248
6496
+
2329856
Fibonacci
144
46368
832040
Friedman
126
128
216
+
995364
frugal
128
256
512
+
10000000
gapful
100
108
120
+
10000000
Gilda
78
220
330
+
5346
Giuga
30
858
1722
66198
happy
28
32
100
+
10000000
harmonic
28
140
270
+
8872200
Harshad
12
18
20
+
10000000
heptagonal
18
112
342
+
9997000
hexagonal
28
66
120
+
9961416
highly composite
12
24
36
+
8648640
hoax
84
160
234
+
9999150
house
32
78
1716
+
9867520
hungry
144
hyperperfect
28
496
8128
iban
12
20
24
+
777744
idoneal
12
16
18
+
1848
impolite
16
32
64
+
8388608
inconsummate
84
216
272
+
999978
insolite
1122112
interprime
12
18
30
+
9999792
Jordan-Polya
12
16
24
+
9953280
junction
204
208
210
+
9999858
Kaprekar
2728
4950
5292
+
8161912
katadrome
20
30
32
+
9876540
Leyland
32
54
100
+
1941760
lonely
120
1344
15704
+
2010800
Lucas
18
5778
Lynch-Bell
12
24
36
+
9867312
magic
260
870
16400
+
8001630
magnanimous
12
16
20
+
115136
metadrome
12
16
18
+
1245678
modest
666
812
888
+
9964482
Moran
18
42
84
+
888
narcissistic
8208
nialpdrome
20
30
32
+
10000000
nonagonal
24
204
396
+
9909504
nude
12
24
36
+
9999936
O'Halloran
12
20
36
+
924
oban
12
16
18
+
990
octagonal
40
96
176
+
9999176
odious
16
28
32
+
9999980
palindromic
66
88
252
+
8992998
pancake
16
56
352
+
9845704
panconsummate
12
18
20
+
144
pandigital
78
108
120
+
9998058
partition
30
42
56
+
8118264
pentagonal
12
176
210
+
9983310
perfect
28
496
8128
pernicious
12
18
20
+
9999980
Perrin
12
90
486
+
2968530
plaindrome
12
16
18
+
6678888
power
16
32
36
+
10000000
powerful
16
32
36
+
10000000
prim.abundant
12
18
20
+
9989312
primorial
30
210
2310
+
9699690
pronic
12
20
30
+
9988760
pseudoperfect
12
18
20
+
1000000
repdigit
66
88
666
+
888888
repfigit
28
1104
2208
+
694280
repunit
40
156
364
+
9984816
Rhonda
1568
4752
5664
+
9541116
Ruth-Aaron
16
24
78
+
9997416
Saint-Exupery
60
480
780
+
9982500
Sastry
528
13224
453288
2975208
self
20
42
64
+
9999840
self-describing
666666
sliding
20
200
520
+
9250000
Smith
378
576
588
+
9997840
sphenic
30
42
66
78
square
16
36
64
+
9998244
straight-line
210
234
420
+
8765432
strobogrammatic
88
96
888
+
9990666
subfactorial
133496
super Niven
12
20
24
+
10000000
super-d
336
348
462
+
9999664
superabundant
12
24
36
+
8648640
tau
12
18
24
+
10000000
taxicab
4104
13832
32832
+
9560896
tetrahedral
20
56
84
+
9962680
tetranacci
56
108
208
+
147312
triangular
28
36
66
+
9965880
tribonacci
24
504
3136
+
8646064
trimorphic
24
624
90624
+
2890624
uban
12
16
18
+
10000000
Ulam
16
18
28
+
9999960
undulating
252
272
414
+
6969696
unprimeable
200
204
208
+
10000000
untouchable
88
96
120
+
999990
upside-down
28
64
456
+
8765432
vampire
1260
1530
6880
+
829696
wasteful
12
18
20
+
9999990
Woodall
80
15624
5764800
Zuckerman
12
24
36
+
9813312
Zumkeller
12
20
24
+
100000
zygodrome
66
88
666
+
9999900