[go: up one dir, main page]
Search a number
amicable numbers
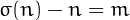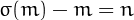Two numbers  $(m,n)$  form an amicable pair if the sum of proper divisors of one number equals the other, i.e., if  $\sigma(n)-n = m$  and  $\sigma(m)-m = n$.

The first numbers which belong to an amicable pair are 220, 284, 1184, 1210, 2620, 2924, 5020, 5564, 6232, 6368, 10744, 10856, 12285, 14595, 17296, 18416, 63020, 66928, 66992 more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
remainders of amicable numbers

A graph displaying how many amicable numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
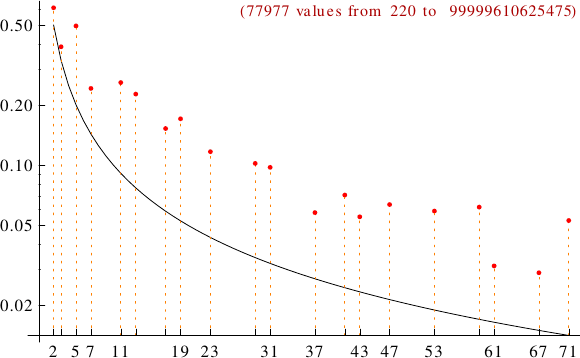
divisibility of amicable numbers
Useful links Mathworld, Amicable Pair
Wikipedia, Amicable number
OEIS, sequence A063990
Amicable numbers can also be... (you may click on names or numbers and on + to get more values)

aban 220 284 169000448 286000065 2688000928 2881000792 4446000368 + 372082000816 460490000260 722254000455 abundant 220 1184 2620 5020 6232 10744 12285 + 48639032 48641584 49215166 alternating 1210 503056 1438983 2941672 2947216 6329416 12101272 + 109410345 365012325 856305272 amenable 220 284 1184 2620 2924 5020 5564 + 998051692 999258676 999728396 apocalyptic 220 2620 2924 5020 5564 6368 10744 + 14595 17296 18416 arithmetic 220 284 2620 2924 5020 5564 6368 + 9660950 9773505 9892936 binomial 220 17296 122265 9363584 congruent 220 284 2620 2924 5020 5564 6232 + 9478910 9592504 9660950 Cunningham 356408 666094293315 Curzon 12285 87633 100485 522405 1077890 1466150 1511930 + 163634510 182622405 188953970 d-powerful 783556 879712 2728726 4238984 5357625 7684672 decagonal 19552219155 deficient 284 1210 2924 5564 6368 10856 14595 + 9592504 9627915 9892936 dig.balanced 1210 2620 12285 124155 171856 202444 503056 + 188953970 196323170 196421715 economical 1184 122368 2090656 9437056 14443730 18017056 18655744 19154336 equidigital 1184 2090656 9437056 14443730 18017056 19154336 esthetic 1210 evil 284 1210 2620 5564 10744 10856 12285 + 993165032 996088412 999258676 frugal 122368 18655744 134886465 169000448 gapful 220 1210 2620 12285 14595 17296 18416 + 97504081155 98645246469 98735418525 Gilda 220 happy 1184 2620 10744 63020 87633 123152 142310 + 7489324 7916696 9892936 Harshad 220 2620 2924 67095 356408 667964 1043096 + 9581473976 9788118628 9844469775 hoax 2924 69615 180848 365084 437456 525915 901424 + 55349570 74055952 84591405 iban 220 1210 10744 142310 202444 inconsummate 5564 10856 66992 123152 180848 203432 319550 + 389924 686072 980984 interprime 1184 10856 12285 17296 71145 122265 430402 + 80422335 86158220 88110536 junction 2620 5020 63020 87633 142310 168730 609928 + 78166448 80422335 97580944 lucky 12285 14595 69615 87633 522405 802725 4482765 modest 280540 360027675 658009485 721522755 nialpdrome 220 87633 88730 nude 1184 odious 220 1184 2924 5020 6232 6368 17296 + 994945490 998051692 999728396 pandigital 1210 124155 525915 9206925 175032884 5209468173 pentagonal 991209208550 pernicious 220 1184 2924 5020 6232 6368 17296 + 9627915 9660950 9892936 persistent 12970438065 84590271368 plaindrome 122368 practical 220 1184 17296 63020 122368 141664 171856 + 6955216 8666860 9363584 prim.abundant 1184 6232 10744 66928 522405 643336 5459176 + 26090325 28118032 34364912 pseudoperfect 220 1184 2620 5020 6232 10744 12285 + 898216 947835 998104 Ruth-Aaron 466417816 self 1210 17296 66928 88730 180848 643336 947835 + 969642056 972264184 991581075 sliding 5020 Smith 66992 879712 1392368 2802416 4238984 7275532 7471508 + 37363095 55349570 91996816 super Niven 220 super-d 71145 142310 185368 319550 783556 1185376 2062570 + 7677248 8666860 9592504 tau 9363584 9437056 25596544 115447424 967887488 tetrahedral 220 17296 9363584 triangular 122265 Ulam 5020 308620 399592 437456 624184 898216 998104 + 4314616 5120595 6377175 unprimeable 6232 10744 66992 67095 69615 88730 123152 + 9627915 9660950 9892936 wasteful 220 284 1210 2620 2924 5020 5564 + 9660950 9773505 9892936 Zuckerman 1184 Zumkeller 220 1184 2620 5020 6232 10744 12285 + 67095 69615 79750