Zeisel numbers

Let us define a sequence as

$\left\{\begin{array}{l} p_0 = 1\\ p_n = a\cdot p_{n-1}+b\,, \end{array}\right.$

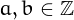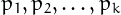where $a,b\in\mathbb{Z}$ . If the numbers $p_1,p_2,\dots,p_k$ are all distinct primes and 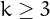$k\ge 3$ , then their product is a Zeisel number.

For example, $1419 = 3\cdot11\cdot43$ is a Zeisel number with parameters $a=4$ and $b=-1$ , because $3 = 4\cdot 1-1$ , $11=4\cdot3-1$ and $43=4\cdot11-1$ .

By construction, the Zeisel numbers are all squarefree.

The smallest Zeisel numbers which are the product of 3, 4, 5 and 6 factors are:

#p	n	factorization	(a,b)
3	105	3 ⋅ 5 ⋅ 7	(1, 2)
4	114985	5 ⋅ 13 ⋅ 29 ⋅ 61	(2, 3)
5	1136972771	11 ⋅ 31 ⋅ 71 ⋅ 151 ⋅ 311	(2, 9)
6	717429818501	11 ⋅ 31 ⋅ 71 ⋅ 151 ⋅ 311 ⋅ 631	(2, 9)

The first Zeisel numbers are 105, 1419, 1729, 1885, 4505, 5719, 15387, 24211, 25085, 27559, 31929, 54205, 59081, 114985, 207177 more terms

Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

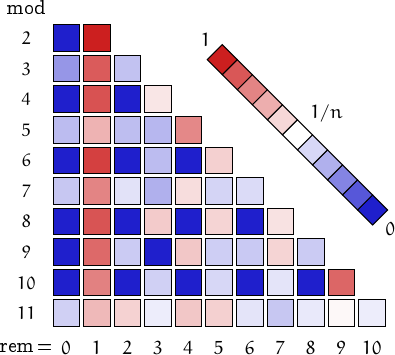
A graph displaying how many Zeisel numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

Useful links Mathworld, Zeisel Number
Wikipedia, Zeisel number
OEIS, Sequence A051015

Zeisel numbers can also be... (you may click on names or numbers and on + to get more values)

aban 105 26000605 524307000169 753601000663 alternating 105 4505 1012121 781296905 amenable 105 1729 1885 4505 25085 31929 54205 59081 + 953055097 970578289 976228129 995762585 apocalyptic 1885 4505 15387 24211 25085 27559 arithmetic 105 1419 1729 1885 4505 5719 15387 24211 + 8712985 8835799 9271805 9773731 binomial 105 Carmichael 1729 294409 56052361 118901521 133800661 172947529 216821881 228842209 + 600613114501 663805468801 727993807201 856666552249 congruent 1419 1885 5719 24211 25085 27559 54205 114985 + 8444431 8712985 8835799 9271805 Cunningham 1729 Curzon 105 4505 59081 15411785 87393129 92458529 cyclic 1729 1885 4505 24211 25085 54205 59081 208681 + 8444431 8712985 9271805 9773731 d-powerful 4293793 5069629 de Polignac 336611 982513 2263811 3973085 8712985 16596371 32894743 34179391 + 52691801 54177877 79796761 96931639 deceptive 1729 294409 56052361 118901521 133800661 172947529 216821881 228842209 + 27278026129 65700513721 71171308081 89951965489 deficient 105 1419 1729 1885 4505 5719 15387 24211 + 8712985 8835799 9271805 9773731 dig.balanced 25085 6173179 8413179 13534129 15411785 54177877 56052361 161164441 172947529 177055201 185245273 double fact. 105 Duffinian 4505 5719 24211 27559 54205 208681 233569 336611 + 8444431 8835799 9271805 9773731 economical 105 233569 1073305 13534129 18175361 equidigital 105 233569 1073305 13534129 18175361 esthetic 1012121 evil 105 1419 1885 4505 5719 15387 25085 27559 + 939947009 970578289 976228129 994732211 gapful 105 1729 1012121 3655861 7355671 14662681 16596371 34179391 + 17141908699 19715531561 36811632961 65092917061 happy 31929 54205 114985 3506371 5069629 6173179 8011459 Harshad 1729 5069629 185245273 222931549 342116741 1017436249 hex 353977 2268651612169 hoax 44544219 iban 24211 207177 idoneal 105 inconsummate 59081 287979 interprime 105 15387 54205 114985 1485609 3077705 4813879 8712985 56052361 junction 105 1419 31929 1012121 13534129 19827641 32894743 48476449 53399449 72730439 79796761 Lehmer 1729 294409 7355671 42501439 56052361 118901521 133800661 172947529 + 663805468801 701432663821 727993807201 856666552249 lucky 105 1419 5719 208681 353977 1073305 8444431 8712985 nialpdrome 8444431 odious 1729 24211 54205 59081 114985 233569 294409 336611 + 873571459 953055097 959646507 995762585 pancake 336611 pandigital 25085 pernicious 1729 54205 114985 233569 353977 1073305 1485609 2953711 + 4293793 7355239 8712985 8835799 plaindrome 233569 Poulet 1729 294409 2953711 26758057 53399449 56052361 96916279 118901521 + 938531360353681 938844932257009 952711345022401 959377262271049 Proth 1729 repunit 1885 Ruth-Aaron 105 self 4505 5719 287979 448585 1485609 2953711 8444431 34179391 + 781296905 820192231 959646507 995762585 Smith 44544219 sphenic 105 1419 1729 1885 4505 5719 15387 24211 + 92458529 92835667 96916279 96931639 super-d 105 1419 5719 31929 59081 208681 233569 336611 + 7558219 8444431 8712985 9773731 taxicab 1729 triangular 105 Ulam 294409 unprimeable 54205 114985 448585 1073305 3077705 3973085 6253085 8712985 wasteful 1419 1729 1885 4505 5719 15387 24211 25085 + 8712985 8835799 9271805 9773731 zygodrome 336611