A number 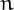 is a Wieferich number if
it holds
is a Wieferich number if
it holds 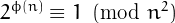 .
.
The formula above, if is a prime, is equivalent
to
, however only two such
numbers, called Wieferich primes are known, namely
1093 and 3511.
The first Wieferich numbers are 1093, 3279, 3511, 7651, 10533, 14209, 17555, 22953, 31599, 42627, 45643, 52665, 68859 more terms
Currently 104 Wieferich numbers are known, the largest being 16547533489305. T. Agoh, K. Dilcher & L. Skula have proved that a larger Wieferich number can exist only if other Wieferich primes exist, apart the 1093 and 3511.
Similarly, two primes and
such that
and
, are called a Wieferich pair.
Only 7 such pairs are known : (2, 1093), (3, 1006003), (5, 1645333507), (5, 188748146801), (83, 4871), (911, 318917), and (2903, 18787).
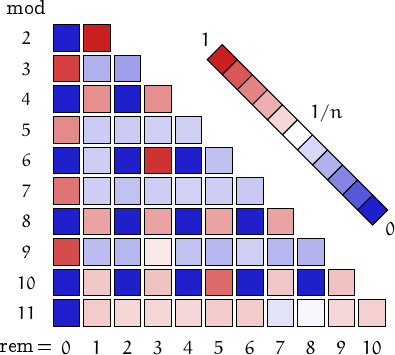
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
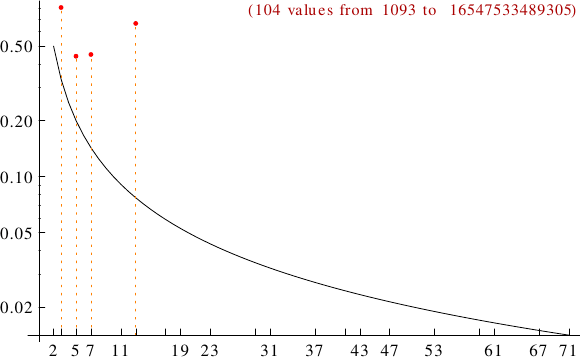
A graph displaying how many Wieferich numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Wieferich numbers can also be... (you may click on names or numbers and on + to get more values)
alternating
298389
410787
1232361
amenable
1093
10533
14209
22953
52665
94797
127881
136929
298389
473985
+
241763949
349214593
518065605
748316985
apocalyptic
3279
3511
7651
10533
14209
17555
22953
arithmetic
1093
3279
3511
7651
10533
14209
17555
22953
42627
45643
+
2053935
2685501
3837523
6161805
binomial
6161805
brilliant
3837523
c.decagonal
3511
Chen
3511
congruent
1093
3279
3511
10533
14209
31599
94797
99463
127881
228215
+
895167
2053935
2685501
6161805
Curzon
10533
52665
127881
298389
6161805
cyclic
1093
3511
3837523
D-number
3279
10533
d-powerful
22953
de Polignac
3837523
deficient
1093
3279
3511
7651
10533
14209
17555
22953
31599
42627
+
2685501
3697083
3837523
6161805
dig.balanced
14209
45643
157995
298389
684645
Duffinian
3279
7651
10533
14209
17555
22953
31599
42627
45643
68859
+
228215
1232361
3697083
3837523
economical
1093
3511
10533
17555
emirp
3511
emirpimes
17555
45643
equidigital
1093
3511
10533
17555
evil
1093
3279
10533
17555
22953
31599
45643
52665
68859
127881
+
349214593
402939915
648541387
725291847
gapful
157995
473985
684645
2685501
6161805
18485415
172688535
1208819745
1346970573
1554196815
+
32638133115
47143970055
60613675785
68096845635
good prime
3511
happy
1093
10533
42627
157995
684645
Harshad
22953
298389
2685501
6161805
172688535
1208819745
1554196815
1945624161
2244950955
3626459235
hex
7651
hoax
2685501
Hogben
22953
inconsummate
94797
127881
473985
interprime
157995
684645
18485415
junction
14209
136929
2053935
57562845
katadrome
7651
lucky
1093
10533
14209
22953
94797
2053935
3697083
Moran
22953
nialpdrome
7651
odious
3511
7651
14209
42627
94797
99463
157995
298389
895167
2053935
+
249438995
448990191
518065605
748316985
panconsummate
1093
pandigital
298389
pernicious
14209
42627
99463
895167
2685501
3697083
6161805
prime
1093
3511
Proth
14209
repunit
1093
22953
self
17555
410787
18485415
26862661
518065605
semiprime
3279
7651
10533
14209
17555
45643
3837523
sphenic
22953
42627
52665
99463
136929
228215
11512569
19187615
26862661
49887799
star
1093
strong prime
3511
super-d
10533
42627
127881
triangular
6161805
twin
1093
Ulam
52665
94797
473985
unprimeable
6161805
wasteful
3279
7651
14209
22953
31599
42627
45643
52665
68859
94797
+
2685501
3697083
3837523
6161805
weak prime
1093