Cullen numbers

Cullen numbers

The

$n$

-th Cullen number is equal to $n\cdot2^n+1$ .

Cullen numbers have been studied because they are seldom prime. They are prime for $n$ = 1, 141, 4713, 5795, 6611, 18496, 32292, 32469, 59656, 90825, 262419,...

The first Cullen numbers are 1, 3, 9, 25, 65, 161, 385, 897, 2049, 4609, 10241, 22529, 49153, 106497, 229377, 491521, 1048577 more terms

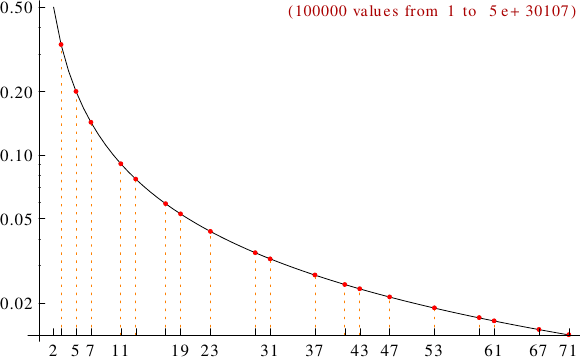
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here

remainders of Cullen numbers

A graph displaying how many Cullen numbers are multiples of the primes p from 2 to 71. In black the ideal line 1/p.

divisibility of Cullen numbers

Useful links Mathworld, Cullen Number
Wikipedia, Cullen number
OEIS, Sequence A002064 Cullen numbers
OEIS, Sequence A005849 Indices of prime Cullen numbers

Cullen numbers can also be... (you may click on names or numbers and on + to get more values)

aban 25 65 161 385 897 alternating 25 65 161 385 amenable 25 65 161 385 897 2049 4609 10241 22529 49153 + 92274689 192937985 402653185 838860801 apocalyptic 2049 4609 10241 22529 arithmetic 65 161 385 897 2049 4609 10241 22529 49153 229377 + 1048577 2228225 4718593 9961473 automorphic 25 brilliant 25 c.octagonal 25 c.square 25 congruent 65 161 49153 Cunningham 65 2049 1048577 3623878657 137438953473 2473901162497 Curzon 65 2049 10241 2228225 cyclic 65 161 2049 22529 49153 491521 1048577 4718593 D-number 2049 d-powerful 2228225 de Polignac 4718593 20971521 44040193 92274689 deficient 25 65 161 385 897 2049 4609 10241 22529 49153 + 1048577 2228225 4718593 9961473 dig.balanced 10241 Duffinian 25 65 161 385 4609 22529 49153 106497 229377 491521 1048577 4718593 economical 25 161 2049 1048577 emirpimes 22529 equidigital 25 161 2049 1048577 esthetic 65 evil 65 897 2049 22529 106497 229377 1048577 9961473 44040193 92274689 838860801 Friedman 25 gapful 385 10241 1048577 2228225 1744830465 32212254721 happy 4609 2228225 Harshad 20971521 iban 10241 idoneal 25 385 inconsummate 65 161 2049 interprime 897 junction 491521 katadrome 65 lucky 25 385 897 4609 magic 65 magnanimous 25 65 metadrome 25 nialpdrome 65 oban 25 65 385 897 octagonal 65 odious 25 161 385 4609 10241 49153 491521 2228225 4718593 20971521 192937985 402653185 palindromic 161 partition 385 pernicious 25 65 161 385 2049 4609 10241 49153 491521 1048577 2228225 4718593 plaindrome 25 power 25 powerful 25 Proth 25 65 161 385 897 2049 4609 10241 22529 49153 + 66571993089 137438953473 283467841537 584115552257 rare 65 Ruth-Aaron 25 self 22529 106497 2228225 402653185 semiprime 25 65 161 2049 4609 22529 1048577 44040193 sliding 25 65 sphenic 385 897 49153 229377 491521 square 25 super-d 106497 229377 trimorphic 25 uban 25 65 undulating 161 wasteful 65 385 897 4609 10241 22529 49153 106497 229377 491521 2228225 4718593 9961473