In its most basic form an 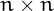 magic square is
an arrangement of the numbers from
magic square is
an arrangement of the numbers from  to
to 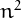 on a square grid in such a way
the entries on the rows, columns and two main diagonals have the same sum.
on a square grid in such a way
the entries on the rows, columns and two main diagonals have the same sum.
![\[
\begin{array}{|c|c|c|}\hline
6 & 7 & 2\\\hline
1 & 5 & 9\\\hline
8 & 3 & 4\\\hline
\end{array}\quad\quad\quad\begin{array}{|c|c|c|c|}\hline
13 & 2 & 3 & 16 \\\hline
8 & 11 & 10 & 5\\\hline
12 & 7 & 6 & 9 \\\hline
1 & 14 & 15 & 4 \\\hline
\end{array}\]](https://speed.lescigales.org/xypor/index.php?q=aHR0cHM6Ly93d3cubnVtYmVyc2FwbGVudHkuY29tL3NldC9tYWdpY19jb25zdGFudC9waWMuOC5wbmc%3D) have magic constant
have magic constant 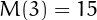 and
and 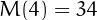 .
.
Magic squares exists for every positive and the common sum, which
we can call magic constant is
.
For example, and
magic squares like these
The first magic constants are 1, 5, 15, 34, 65, 111, 175, 260, 369, 505, 671, 870, 1105, 1379, 1695, 2056, 2465, 2925, 3439 more terms
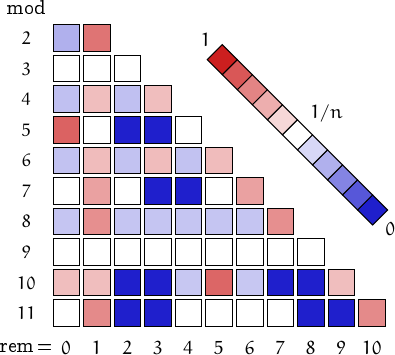
Pictorial representation of remainders (mod 2, 3, ...,11) frequency. For a table of values and more details click here
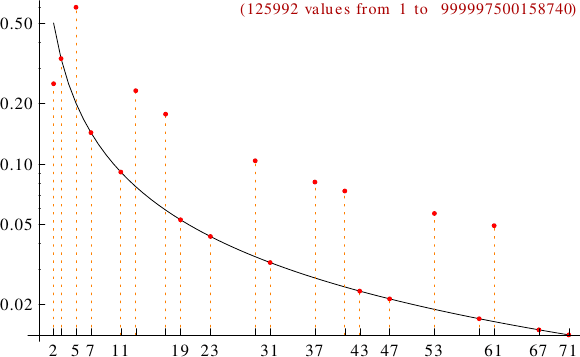
A graph displaying how many magic constants are multiples of the primes p from 2 to 71. In black the ideal line 1/p.
Magic constants can also be... (you may click on names or numbers and on + to get more values)
aban
15
34
65
+
928166000645
abundant
260
870
6924
+
48668230
admirable
87836
alternating
34
65
369
+
727210385
amenable
65
260
369
+
995433385
apocalyptic
671
1105
1695
+
29679
arithmetic
15
65
111
+
9951391
astonishing
15
Bell
15
binomial
15
2925
brilliant
15
671
c.pentagonal
2287231
c.square
1105
cake
15
Carmichael
1105
2465
congruent
15
34
65
+
9951391
constructible
15
34
2056
8388736
Cullen
65
Cunningham
15
65
73599240
Curzon
65
369
870
+
193710609
cyclic
15
65
671
+
9951391
D-number
15
111
d-powerful
175
2465
66351
+
5848655
de Polignac
2465
78759
102719
+
80939585
decagonal
175
1105
deceptive
14911
1826209
deficient
15
34
65
+
9951391
dig.balanced
15
260
8801
+
199344496
double fact.
15
Duffinian
65
111
175
+
9951391
eban
34
2056
32000002000
economical
15
111
175
+
18797855
emirpimes
15
1379
12209
+
93084991
equidigital
15
111
175
+
18797855
eRAP
4969188575
esthetic
34
65
evil
15
34
65
+
997809119
fibodiv
66351
Fibonacci
34
Friedman
125055
256040
265761
+
976625
frugal
6826079
161414771
193710609
609093750
gapful
260
671
1695
+
99230675185
happy
671
5335
8801
+
9095855
Harshad
111
870
2465
+
9885306184
heptagonal
34
19669
hex
14911
hexagonal
15
hoax
27455
143781
578865
+
93574910
Hogben
111
iban
111
4010
idoneal
15
inconsummate
65
4641
21455
+
976625
insolite
111
interprime
15
34
111
+
91625500
junction
111
505
2925
+
72766051
katadrome
65
870
Lehmer
15
1105
1695
+
910382081071
Leyland
4294968320
lucky
15
111
1105
+
9951391
Lynch-Bell
15
175
magnanimous
34
65
2465
8801
metadrome
15
34
369
1379
modest
111
21621951
Moran
111
3439
23346
nialpdrome
65
111
870
+
665555
nonagonal
111
nude
15
111
175
+
336111126
O'Halloran
260
oban
15
65
369
+
870
octagonal
65
2465
odious
369
505
671
+
995433385
palindromic
111
505
5335
pancake
1379
panconsummate
15
34
pandigital
15
210975
partition
15
pernicious
34
65
260
+
9841635
persistent
51646873290
plaindrome
15
34
111
+
23346
Poulet
1105
2465
6998881
139101047324161
practical
260
870
16400
+
8001630
prim.abundant
87836
primeval
1379
pronic
870
Proth
65
25345
364545
pseudoperfect
260
870
6924
+
864060
rare
65
repdigit
111
repunit
15
111
Ruth-Aaron
15
369
44657535
150381835
self
1379
4641
6924
+
981258130
semiprime
15
34
65
+
93084991
sliding
65
Smith
143781
578865
629910
+
96550565
sphenic
1105
1695
2465
+
98061761
straight-line
111
369
strobogrammatic
111
super Niven
500050
4000100
500000500
4000001000
super-d
369
7825
19669
+
9410681
tau
2056
6924
2048080
+
702464560
tetrahedral
2925
tetranacci
15
triangular
15
uban
15
65
Ulam
175
260
2056
+
8889921
undulating
505
unprimeable
6924
16400
21455
+
9841635
untouchable
16400
32020
296394
+
629910
upside-down
1379
wasteful
34
65
260
+
9951391
weird
10990
Zuckerman
15
111
175
Zumkeller
260
870
6924
+
87836
zygodrome
111
665555
665500005500
665500000055000