Dış merkezlik (astronomi)


| Yörünge mekaniği |
|---|
 |
Astrodinamikte, bir astronomik cismin yörünge eksantrikliği (dış merkezlilik), başka cisim etrafındaki yörüngesinin mükemmel bir daireden ne kadar saptığını belirleyen boyutsuz bir parametredir.
0 değeri dairesel yörünge olup 0 ile 1 arasındaki değerler eliptik bir yörünge çizer, 1 ise parabolik kaçış yörüngesi (veya yakalama yörüngesidir) ve 1'den büyük değerler hiperboldür.
Her Kepler yörüngesi bir konik kesit olduğundan, terim adını konik kesitlerin parametrelerinden alır. Normalde izole edilmiş iki cisim problemi için kullanılır, ancak Galaksi boyunca bir rozet yörüngesini takip eden nesneler için uzantılar da vardır.
Tanım
[değiştir | kaynağı değiştir]Ters-kare-yasa kuvvetine sahip iki cisim probleminde, her yörünge bir Kepler yörüngesidir. Bu Kepler yörüngesinin eksantrikliği, şeklini tanımlayan negatif olmayan bir sayıdır.
Eksantriklik aşağıdaki değerleri alabilir:
Dairesel yörünge: e = 0
Eliptik yörünge: 0 < e < 1
Parabolik yörünge: e = 1
Hiperbolik yörünge: e > 1
Eksantriklik (e) şu şekilde hesaplanır:
Burada E toplam yörünge enerjisi, L açısal momentum, mred indirgenmiş kütle ve α klasik fizikteki yerçekimi veya elektrostatik teorisinde olduğu gibi ters-kare yasası merkezi kuvvet katsayısıdır:
( Bu, çekici bir kuvvet için negatif, itici bir kuvvet için pozitiftir; Kepler problemi ile ilgilidir.)
veya yerçekimi kuvveti durumunda;
burada ε özgül yörünge enerjisi (toplam enerjinin indirgenmiş kütleye bölümü), μ toplam kütleye dayalı standart yerçekimi parametresi ve h özgül göreli açısal momentumdur (açısal momentumun indirgenmiş kütleye bölümü).[3]
0'dan 1'e kadar olan e değerleri için yörüngenin şekli giderek uzayan (veya düzleşen) bir elipstir;
1'den sonsuza kadar olan e değerleri için yörünge, 180'den 0 dereceye azalan 2 arccsc(e) toplam dönüş yapan bir hiperbol dalıdır.
Burada toplam dönüş, dönüş sayısına benzer ancak açık eğriler (hız vektörü tarafından kapsanan açıdır) içindir. Elips ve hiperbol arasındaki sınır durum, e=1 olduğundaki paraboldür.
Radyal yörüngeler, eksantrikliğe göre değil yörüngenin enerjisine göre eliptik, parabolik veya hiperbolik olarak sınıflandırılır. Radyal yörüngelerin açısal momentumu sıfırdır dolayısıyla bire eşit eksantrikliği vardır. Enerji sabit tutulup açısal momentum azaltıldığında eliptik, parabolik ve hiperbolik yörüngelerin her biri karşılık gelen radyal yörünge tipine yönelirken e=1' e yönelir (veya parabolik durumda 1 olarak kalır).
İtici bir kuvvet için, radyal versiyon da dahil olmak üzere sadece hiperbolik yörünge geçerlidir.
Eliptik yörüngeler için basit bir kanıt; 'nin mükemmel dairenin eksantrikliği e olan elips'e izdüşüm açısı verdiğini gösterir.
Örneğin, Merkür gezegeninin eksantrikliğini (e = 0,2056) görmek üzere, 11,86 derece izdüşüm açısını bulmak için ters sinüsü hesaplamak yeterlidir. Sonra herhangi dairesel nesneyi bu açıyla eğildiğinde, izleyicinin gözüne yansıtılan bu nesnenin görünen elipsi aynı eksantrikliğe sahip olur.
Örnekler
[değiştir | kaynağı değiştir]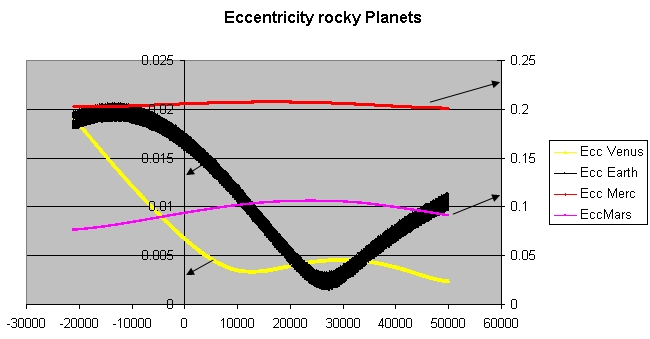
Dünya'nın yörünge eksantrikliği yaklaşık 0,0167'dir ve yörüngesi neredeyse daireseldir. Venüs ve Neptün'ün eksantriklikleri daha da azdır. Yüz binlerce yıl boyunca Dünya yörünge eksantrikliği, gezegenler arasındaki yerçekiminin sonucunda yaklaşık 0,0034 ile neredeyse 0,058 arasında değişmiştir.[4]
| Cisim | Dışmerkezlik |
|---|---|
| Triton | 0,00002 |
| Venus | 0,0068 |
| Neptün | 0,0086 |
| Dünya | 0,0167 |
| Titan | 0,0288 |
| Uranüs | 0,0472 |
| Jüpiter | 0,0484 |
| Satürn | 0,0541 |
| Ay | 0,0549 |
| 1 Ceres | 0,0758 |
| 4 Vesta | 0,0887 |
| Mars | 0,0934 |
| 10 Hygiea | 0,1146 |
| Makemake | 0,1559 |
| Haumea | 0,1887 |
| Merkür | 0,2056 |
| 2 Pallas | 0,2313 |
| Pluto | 0,2488 |
| 3 Juno | 0,2555 |
| 324 Bamberga | 0,3400 |
| Eris | 0,4407 |
| Nereid | 0,7507 |
| Sedna | 0,8549 |
| Halley Kuy. Yıl. | 0,9671 |
| Hale-Bopp Kuy. Yıl | 0,9951 |
| Ikeya-Seki Kuy. Yıl. | 0,9999 |
| C/1980 E1 | 1,057 |
| ʻOumuamua | 1,20[a] |
| C/2019 Q4 (Borisov) | 3,5 [b] |
Tabloda tüm gezegenler ve cüce gezegenler ile seçilmiş asteroitler, kuyruklu yıldızlar ve uydular için değerler listelenmektedir. Merkür'ün, Güneş Sistemi'ndeki herhangi bir gezegenden daha büyük yörünge eksantrikliği vardır (e = 0,2056). Bu eksantriklik, Merkür'ün perihelion'da aphelion'a kıyasla iki kat daha fazla güneş radyasyonu alması için yeterlidir.
2006'da gezegen statüsünden düşürülmeden önce, Plüton en eksantrik yörüngeli gezegen olarak kabul ediliyordu (e = 0,248).
Diğer Neptün ötesi nesneler, özellikle cüce gezegen Eris (0,44) eksantrikliğ vardır. Daha da uzaktaki Sedna'nın tahmini 937 AU enöte ve yaklaşık 76 AU enberi nedeniyle 0,855 gibi çok büyük eksantrikliği vardır.
Güneş Sistemi'ndeki asteroitlerin çoğunun yörünge eksantriklikleri 0 ile 0,35 arasında olup ortalama değer 0,17'dir.[5] Nispeten büyük eksantriklikleri muhtemelen Jüpiter'in etkisinden ve geçmişteki çarpışmalardan kaynaklanır.
Ay'ın değeri 0,0549 olup, Güneş Sistemi'nin büyük uyduları arasında en eksantriklisidir. Dört Galilei uydusunun eksantrikliği 0,01'den daha azdır.
Neptün'ün en büyük uydusu Triton'un eksantrikliği 1,6×10-5'dir. (0,000016),[6] Güneş Sistemi'ndeki bilinen uydular arasında en küçük eksantrikli olandır; yörüngesi mükemmel bir daire gibidir. Ancak, daha küçük uyduların, özellikle Neptün'ün üçüncü büyük uydusu Nereid (0,75) gibi düzensiz uyduların önemli eksantriklikleri olabilir.
Kuyruklu yıldızlar çok farklı eksantrik değerlidir. Periyodik kuyruklu yıldızların eksantriklikleri çoğunlukla 0,2 ile 0,7 arasındadır[7] ancak bazılarının eksantriklikleri 1'in biraz altında olup oldukça eksantrik eliptik yörüngelidir; örneğin Halley Kuyruklu Yıldızı 0,967 değerlidir.
Periyodik olmayan kuyruklu yıldızlar neredeyse parabolik yörünge izler ve bu nedenle 1'e daha da yakın eksantriklikleri vardır. 0,995 değerli Hale-Bopp kuyruklu yıldızı[8] ve 1,000019 değerli C/2006 P1 (McNaught) kuyruklu yıldızı bunun örekleridir.[9] Hale–Bopp'un değeri 1'den küçük olduğunda yörüngesi eliptiktir ve sisteme geri dönecektir.[8]
McNaught gezegenlerin etkisi altındayken hiperbolik bir yörüngeliidir[9] ancak yine de yaklaşık 105 yıllık bir yörünge periyoduyla Güneş'e bağlıdır.[10] C/1980 E1 Kuyruklu Yıldızı 1,057 eksantriklik ile Güneş kökenli bilinen hiperbolik kuyruklu yıldızlar arasında en büyük eksantrikliğe sahiptir,[11] ve sonunda Güneş Sistemi'ni terk edecektir.
ʻOumuamua, Güneş sistemi'nden geçtiği tespit edilen ilk yıldızlararası nesne'dir. Yörünge dış merkezliliğinin 1,20 olması, ʻOumuamua'nın Güneş'e hiçbir zaman kütleçekimsel olarak bağlı olmadığını gösterir. Dünya'dan 0,2 AU (30000000 km; 19000000 mi) uzaklıkta keşfedilmiştir ve yaklaşık 200 metre çapındadır. Yıldızlararası hızı (sonsuzdaki hızı) 26,33 km/s (58900 mph)'dir.
Ortalama eksantriklik
[değiştir | kaynağı değiştir]Bir nesnenin ortalama eksantrikliği, belirli bir zaman aralığında pertürbasyonlar sonucu oluşan ortalama eksantrikliktir. Neptün'ün halen 0,0113 anlık (güncel devir) eksantrikliği vardır[12] ancak 1800'den 2050'ye kadar ortalama eksantriklik 0,00859'dur.[13]
İklimsel etki
[değiştir | kaynağı değiştir]Yörünge mekaniği, mevsimlerin süresinin Dünya'nın yörüngesinin gündönümleri ve ekinokslar arasında taranan alanıyla orantılı olmasını gerektirir. Bu nedenle yörünge eksantrikliği aşırı olduğunda, yörüngenin uzak tarafında (enöte) meydana gelen mevsimlerin süresi çok daha uzun olabilir. Kuzey yarımkürede sonbahar ve kış, Dünya'nın maksimum hızda hareket ettiği en yakın yaklaşmada (enberi) meydana gelirken, güney yarımkürede bunun tam tersi olur. Sonuçta, kuzey yarımkürede sonbahar ve kış, ilkbahar ve yazdan biraz daha kısadır; ancak küresel anlamda bu durum ekvatorun altında daha uzun olmaları ile dengelenir. 2006 yılında Milankovitch döngüleri nedeniyle kuzey yarımkürede yaz, kıştan 4,66 gün, ilkbahar ise sonbahardan 2,9 gün daha uzundu.[14][15]
Kubbemsi yalpalanma da Dünya'nın yörüngesinde gündönümlerini ve ekinoksların oluştuğu yeri yavaşça değiştirir. Bu, yörüngesel salınım da denilen dönme ekseninde değil, Dünya'nın yörüngesindeki yavaş bir değişimdir. Önümüzdeki 10000 yıl boyunca, kuzey yarımkürede kışlar giderek uzayacak ve yazlar kısalacaktır. Ancak, bir yarımküredeki soğuma etkisi diğer yarımküredeki ısınma ile dengelenecek ve Dünya'nın yörüngesinin eksantrikliğinin neredeyse yarı yarıya azalacak olması nedeniyle genel değişikliklere karşı koyulacaktır.[16] Bu durum ortalama yörünge yarıçapını azaltacak ve her iki yarımküredeki sıcaklıkları orta buzul zirvesine yaklaştıracaktır.
Dış Gezegenler
[değiştir | kaynağı değiştir]Keşfedilen birçok ötegezegenin çoğu Güneş sistemi'ndeki gezegenlerden daha çok yörünge eksantriklikleri vardır. Az yörünge eksantrikliği olan (dairesele yakın yörüngeler) ötegezegenler yıldızlarına çok yakındır ve yıldıza kütleçekim kilidi durumdadır.
Güneş Sistemi'ndeki sekiz gezegenin tümü dairesele yakın yörüngeliidir. Keşfedilen ötegezegenler, alışılmadık derecede az eksantriklikte Güneş Sistemi'nin nadir ve benzersiz olduğunu gösterir.[17] Bir teori bu az eksantrikliği Güneş Sistemi'ndeki çok sayıda gezegene bağlarken; bir diğeri bunun benzersiz asteroit kuşakları nedeniyle ortaya çıktığını öne sürer. Başka çok gezegenli sistemler de bulunmuştur ancak hiçbiri Güneş Sistemi'ne benzemez. Güneş Sistemi, gezegenlerin neredeyse dairesel yörüngeli olmasına yol açan benzersiz planetesimal sistemlere sahiptir.
Güneş sistemindeki gezegenimsi sistemler asteroid kuşağı, Hilda ailesi, Kuiper kuşağı, Hills bulutu ve Oort bulutu'nu içerir. Keşfedilen ötegezegen sistemlerinde ya hiç gezegenimsi sistem yoktur ya da çok büyük bir tane vardır. Yaşanabilirlik özellikle de gelişmiş yaşam için az eksantriklik gereklidir.[18] Çok sayıda gezegen sistemlerinin yaşanabilir ötegezegenleri olma olasılığı daha çoktur.[19][20] Güneş Sistemi'ne ilişkin Büyük göç hipotezi, dairesel yörüngelerini ve diğer benzersiz özelliklerini anlamaya da yardımcı olur.[21][22][23][24][25][26][27][28]
Ayrıca bakınız
[değiştir | kaynağı değiştir]Notlar
[değiştir | kaynağı değiştir]- ^ Oumuamua hiçbir zaman Güneş'e bağlı olmamıştır, bu nedenle yörüngesi hiperboliktir: e ≈ 1.20 > 1 .
- ^ C/2019 Q4 (Borisov) hiçbir zaman Güneş'e bağlı olmamıştır, bu nedenle yörüngesi hiperboliktir: e ≈ 3,5 >> 1 .
Kaynakça
[değiştir | kaynağı değiştir]- ^ Abraham, Ralph (2008). Foundations of mechanics (2.2diğerleri=Jerrold E. Marsden bas.). Providence, R.I.: AMS Chelsea Pub./American Mathematical Society. ISBN 978-0-8218-4438-0. OCLC 191847156.
- ^ Bate et al. 2020, s. 24.
- ^ Bate et al. 2020, ss. 12–17.
- ^ A. Berger; M.F. Loutre (1991). "Graph of the eccentricity of the Earth's orbit". Illinois State Museum (Insolation values for the climate of the last 10 million years). 6 Ocak 2018 tarihinde kaynağından arşivlendi.
- ^ "Asteroids". web.archive.org. 4 Mart 2007. 4 Mart 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Nisan 2023.
- ^ David R. Williams (22 Ocak 2008). "Neptün Uydusu Bilgi Formu". NASA. 19 Aralık 1996 tarihinde kaynağından arşivlendi.
- ^ Lewis, John (2 Aralık 2012). Physics and Chemistry of the Solar System. Academic Press. ISBN 9780323145848.
- ^ a b "JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)" (2007-10-22 last obs). 19 Ağustos 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Aralık 2008.
- ^ a b "JPL Small-Body Database Browser: C/2006 P1 (McNaught)" (2007-07-11 last obs). 5 Aralık 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Aralık 2009.
- ^ "Comet C/2006 P1 (McNaught) - facts and figures". Perth Observatory in Australia. 22 Ocak 2007. 18 Şubat 2011 tarihinde kaynağından arşivlendi.
- ^ "JPL Küçük Gövde Veritabanı Tarayıcısı: C/1980 E1 (Bowell)" (1986-12-02 son gözlem). 12 Mayıs 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Mart 2010.
- ^ Williams, David R. (29 Kasım 2007). "Neptün Bilgi Formu". NASA. 19 Aralık 1996 tarihinde kaynağından arşivlendi.
- ^ "S.S. 1800'den 2050'ye kadar olan dönem için Seplerian elementler". JPL Güneş Sistemi Dinamiği. 22 Eylül 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 17 Aralık 2009.
- ^ "Earth's Seasons". web.archive.org. 13 Ekim 2007. 21 Mart 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Nisan 2023.
- ^ Berger A.; Loutre M.F.; Mélice J.L. (2006). "Ekvatoral güneşlenme: presesyon harmoniklerinden eksantriklik frekanslarına" (PDF). Clim. Past Discuss. 2 (4): 519-533. doi:10.5194/cpd-2-519-2006. 12 Mayıs 2013 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 4 Nisan 2023.
- ^ "Long Term Climate". ircamera.as.arizona.edu. 4 Mayıs 2007 tarihinde kaynağından arşivlendi.
- ^ "ECCENTRICITY". exoplanets.org. 22 Ocak 2001 tarihinde kaynağından arşivlendi.
- ^ Ward, Peter; Brownlee, Donald (2000). Rare Earth: Why Complex Life is Uncommon in the Universe. Springer. ss. 122-123. ISBN 0-387-98701-0.
- ^ Limbach, MA; Turner, EL (2015). "Exoplanet orbital eccentricity: multiplicity relation and the Solar System". Proc Natl Acad Sci U S A. 112 (1): 20-4. arXiv:1404.2552 $2. Bibcode:2015PNAS..112...20L. doi:10.1073/pnas.1406545111. PMC 4291657 $2. PMID 25512527.
- ^ Youdin, Andrew N.; Rieke, George H. (15 Aralık 2015). "Planetesimals in Debris Disks". arXiv:1512.04996 $2.
- ^ Zubritsky, Elizabeth. "Jupiter's Youthful Travels Redefined Solar System". NASA. 9 Haziran 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Kasım 2015.
- ^ Sanders, Ray (23 Ağustos 2011). "How Did Jupiter Shape Our Solar System?". Universe Today. 22 Eylül 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Kasım 2015.
- ^ Choi, Charles Q. (23 Mart 2015). "Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System". Space.com. 23 Mart 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Kasım 2015.
- ^ Davidsson, Dr. Björn J. R. "Mysteries of the asteroid belt". The History of the Solar System. 14 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Kasım 2015.
- ^ Raymond, Sean (2 Ağustos 2013). "The Grand Tack". PlanetPlanet. 12 Nisan 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Kasım 2015.
- ^ O'Brien, David P.; Walsh, Kevin J.; Morbidelli, Alessandro; Raymond, Sean N.; Mandell, Avi M. (2014). "Water delivery and giant impacts in the 'Grand Tack' scenario". Icarus. 239: 74-84. arXiv:1407.3290 $2. Bibcode:2014Icar..239...74O. doi:10.1016/j.icarus.2014.05.009.
- ^ Loeb, Abraham; Batista, Rafael; Sloan, David (August 2016). "Relative Likelihood for Life as a Function of Cosmic Time". Journal of Cosmology and Astroparticle Physics. 2016 (8): 040. arXiv:1606.08448 $2. Bibcode:2016JCAP...08..040L. doi:10.1088/1475-7516/2016/08/040.
- ^ "Is Earthly Life Premature from a Cosmic Perspective?". Harvard-Smithsonian Center for Astrophysics. 1 Ağustos 2016.
{{
| Astronomi ile ilgili bu madde taslak seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |